How a 7-Million Parameter Model Beats GPT, Gemini, and Claude at Reasoning [Breakdowns]
How Samsung invented a new way of thinking for LLMs with the Tiny Recursive Model.
It takes time to create work that’s clear, independent, and genuinely useful. If you’ve found value in this newsletter, consider becoming a paid subscriber. It helps me dive deeper into research, reach more people, stay free from ads/hidden agendas, and supports my crippling chocolate milk addiction. We run on a “pay what you can” model—so if you believe in the mission, there’s likely a plan that fits (over here).
Every subscription helps me stay independent, avoid clickbait, and focus on depth over noise, and I deeply appreciate everyone who chooses to support our cult.
PS – Supporting this work doesn’t have to come out of your pocket. If you read this as part of your professional development, you can use this email template to request reimbursement for your subscription.
Every month, the Chocolate Milk Cult reaches over a million Builders, Investors, Policy Makers, Leaders, and more. If you’d like to meet other members of our community, please fill out this contact form here (I will never sell your data nor will I make intros w/o your explicit permission)- https://forms.gle/Pi1pGLuS1FmzXoLr6
Large Language Models continue to make breakthroughs in their ability to synthesize knowledge, generate fluent text, and recognize complex patterns. Yet, for all their scale, they harbor a fundamental architectural flaw that renders them unreliable for tasks requiring verifiable, multi-step reasoning. Their autoregressive, single-pass generation process — making one irreversible decision at a time — is profoundly ill-suited for logic puzzles, complex planning, or formal proofs, where a single early error invalidates the entire solution.
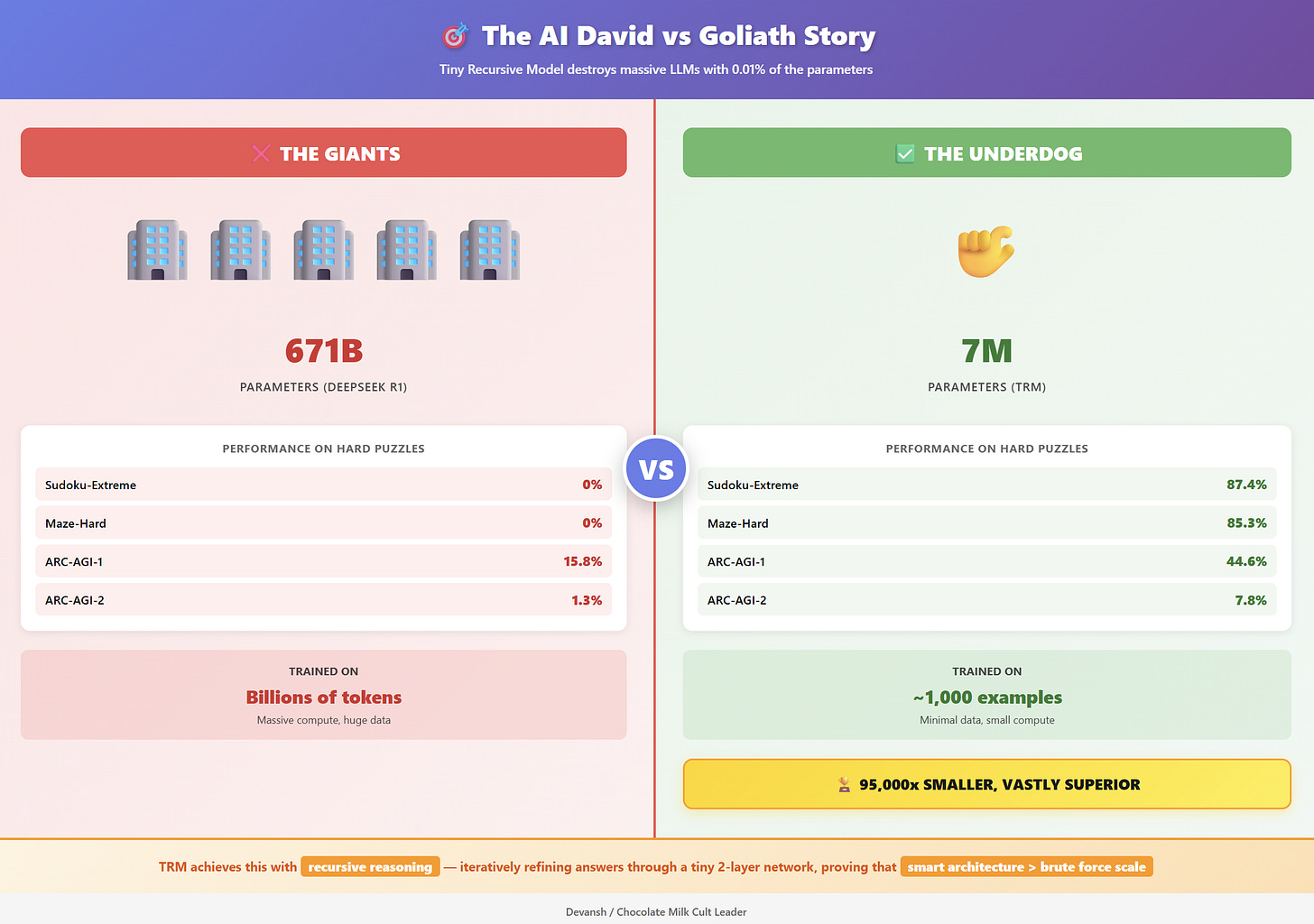
A new paper, “Less is More: Recursive Reasoning with Tiny Networks,” presents a direct and powerful challenge to this paradigm. It details the Tiny Recursive Model (TRM), an architecture that redefines the relationship between size and capability. The results are stark: “With only 7M parameters, TRM obtains 45% test-accuracy on ARC-AGI-1 and 8% on ARC-AGI-2, higher than most LLMs (e.g., Deepseek R1, o3-mini, Gemini 2.5 Pro) with less than 0.01% of the parameters.”
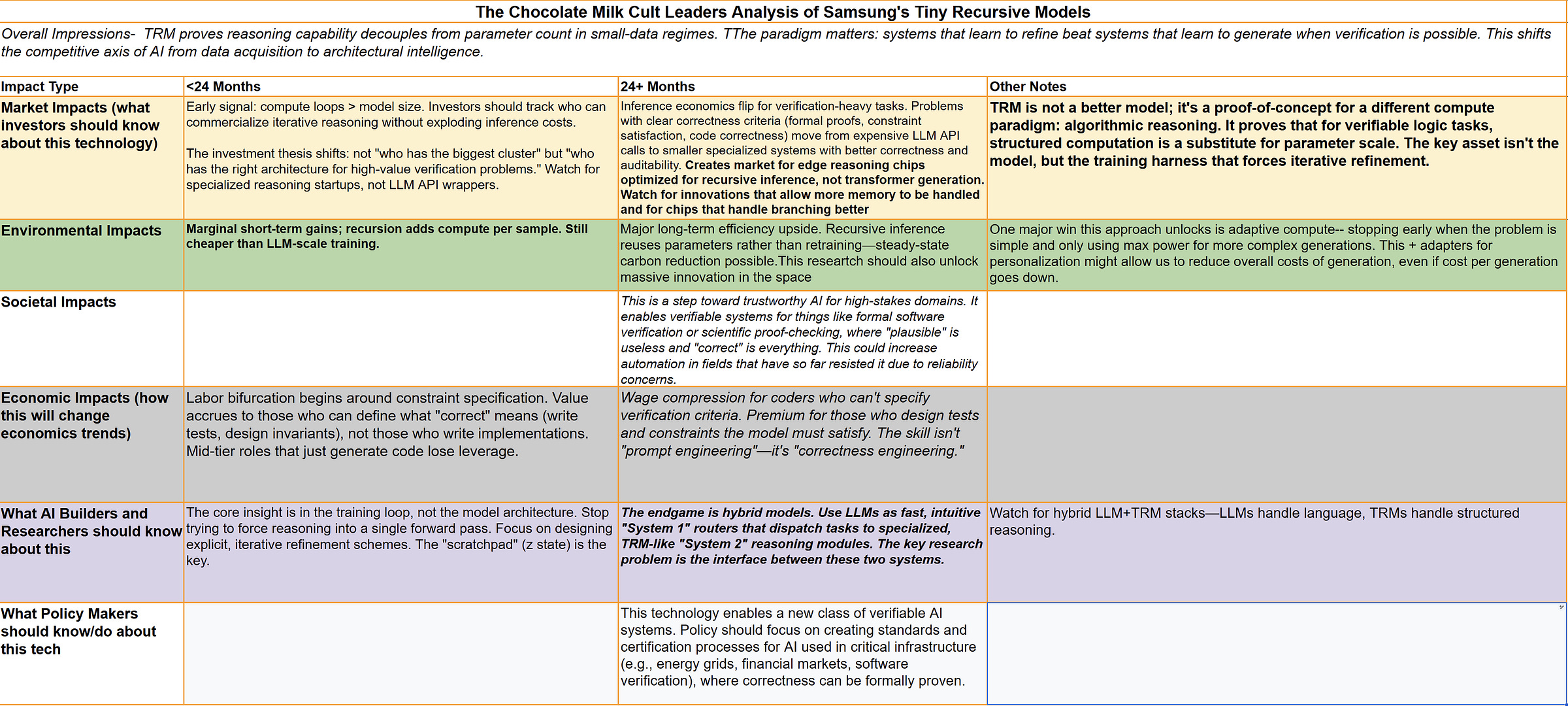
The success of TRM proves that for a critical class of reasoning problems, the algorithmic structure of computation is a more powerful driver of performance than the sheer scale of compressed knowledge. It argues that how a model thinks is more important than what it knows, an approach that will has several important implications for how we think and how next-gen AI systems will balance context retrieval, ranking, and analysis.
In this deep dive, we go deep into this breakthrough. We will cover:
The Foundational Principles of Iterative Reasoning: We will establish from first principles why thinking in loops — and separating a proposed ‘answer’ from a ‘reasoning scratchpad’ — is the essential algorithmic shift required to solve complex logical problems.
A Detailed Breakdown of the TRM Architecture: We will dissect the specific design choices that enable TRM’s performance, from its elegant, unified network that handles both reasoning and answering, to its principled training method that provides a precise learning signal.
A Multi-Dimensional Analysis of TRM’s Impact: We will examine the strategic implications of this new paradigm, covering its potential to reshape AI research trajectories, create new engineering patterns for specialized models, and unlock novel investment opportunities in “algorithmic AI.”
An Honest Assessment of Limitations and Future Directions: Finally, we will address the current constraints of the TRM approach and look toward the future research it inspires, from dynamic computation to the creation of hybrid AI systems that combine the strengths of both large and small models.
Slip into something comfy, get your hall passes out, because we are going to get very intimate with this research.
Executive Highlights (TL;DR of the Article)
Large Language Models can write, translate, and summarize — but they can’t reason. Their architecture makes one decision at a time, with no way to revise. Once they go wrong, they stay wrong.
Samsung’s Tiny Recursive Model (TRM) flips that logic. Instead of generating answers once, it thinks in loops — revising, checking, and improving its output over multiple passes. With only 7 million parameters, TRM outperforms trillion-parameter LLMs on hard reasoning benchmarks like ARC-AGI and Sudoku-Extreme.
The Core Innovation:
TRM separates reasoning (its latent thought process, z) from answers (its visible output, y). It updates both repeatedly — like a mathematician checking their work. Each iteration uses real gradients (no approximations), giving the model a perfect learning signal. The result is a small network that learns procedures instead of memorizing examples.
Key Design Choices:
Nested Loops: Inner loops perform micro-reasoning; outer loops perform macro-correction.
Algorithmic Regularization: Only two transformer layers — small enough to force generalization.
Exact Gradients: Full backpropagation through recursion for fidelity over convenience.
Simple Halting & EMA: One binary “am I done?” check and exponential moving averages keep training stable.
Why It Matters:
TRM proves intelligence doesn’t require scale — it requires structure.
For Research: Shifts focus from parameter growth to algorithmic depth and reasoning loops.
For Engineering: Enables small, specialist “reasoning coprocessors” that can verify and refine outputs.
For Investment: Opens a new frontier — algorithmic AI, where insight, not infrastructure, drives value.
Limits: TRM is slow, task-specific, and relies on supervised data. Future work aims at dynamic recursion (models that decide when to stop thinking), hybrid systems combining LLM perception with TRM reasoning, and self-critiquing architectures that learn without labels.
The Big Idea: LLMs compress knowledge; TRMs learn computation.
One remembers the world. The other learns how to reason about it. This marks the beginning of AI’s next era — from memory to recursion, where intelligence is defined not by what a model knows, but by how gracefully it can change its own mind.
I put a lot of work into writing this newsletter. To do so, I rely on you for support. If a few more people choose to become paid subscribers, the Chocolate Milk Cult can continue to provide high-quality and accessible education and opportunities to anyone who needs it. If you think this mission is worth contributing to, please consider a premium subscription. You can do so for less than the cost of a Netflix Subscription (pay what you want here).
I provide various consulting and advisory services. If you‘d like to explore how we can work together, reach out to me through any of my socials over here or reply to this email.
Part 2: The Algorithmic Foundation of Iterative Reasoning
The Challenge: From Single-Pass Generation to Multi-Step Deduction
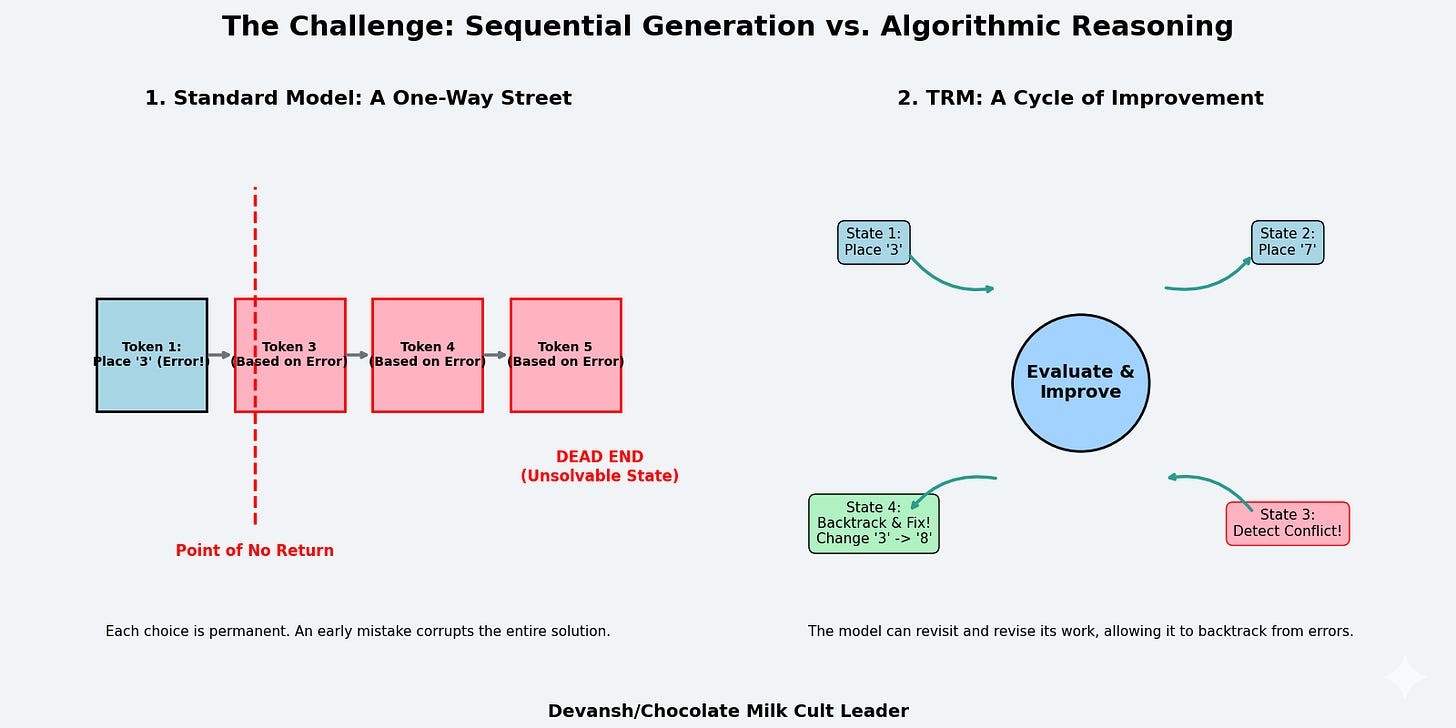
LLMs generate solutions sequentially. The model predicts token t₁, commits to it, uses it as context to predict t₂, commits, and continues. Each decision is made once. There’s no revision mechanism.
But consider solving a Sudoku puzzle. You place a 3 in row 2, column 4. This choice propagates constraints across the entire grid — now column 4 can’t have another 3, now the top-middle box can’t have another 3, now row 2’s remaining cells must contain 1,2,4,5,6,7,8,9. If that initial 3 was wrong, every subsequent placement is working from corrupted constraints. The error compounds. By the time you’ve filled 20 cells, the puzzle is unsolvable, but the model has no mechanism to recognize this and backtrack (specifically, it won’t have a good way to identify where the thinking went wrong/where it should reset to).
Get that tattooed —a fundamental issue for LLMs in complex reasoning is irreversibility. LLMs can generate a “chain of thought” before their final answer — a sequence of reasoning tokens that walk through the problem. But this is still a single forward pass. The model generates “Let me think step by step: first I’ll try placing 3 in row 2, column 4, then…” and continues. If step 3 reveals that step 1 was wrong, the model can’t go back and revise step 1. It’s already sampled those tokens and moved on.
In other words, bad paths will continue to influence the latent space generations, potentially compromising the quality of all future generations in that chat session.
This limitation appears across every task that requires:
Backtracking: exploring a path, discovering it’s wrong, returning to a branch point
Constraint propagation: where early decisions create complex downstream implications
Verification loops: checking your work and revising based on discovered errors
Multi-step planning: where the full solution requires coordinating many interdependent decisions
These are precisely the tasks where even massive LLMs fail completely. These aren’t knowledge problems. They’re algorithmic problems that require a whole new approach, one that is more active with its learning.
Let’s understand that next.
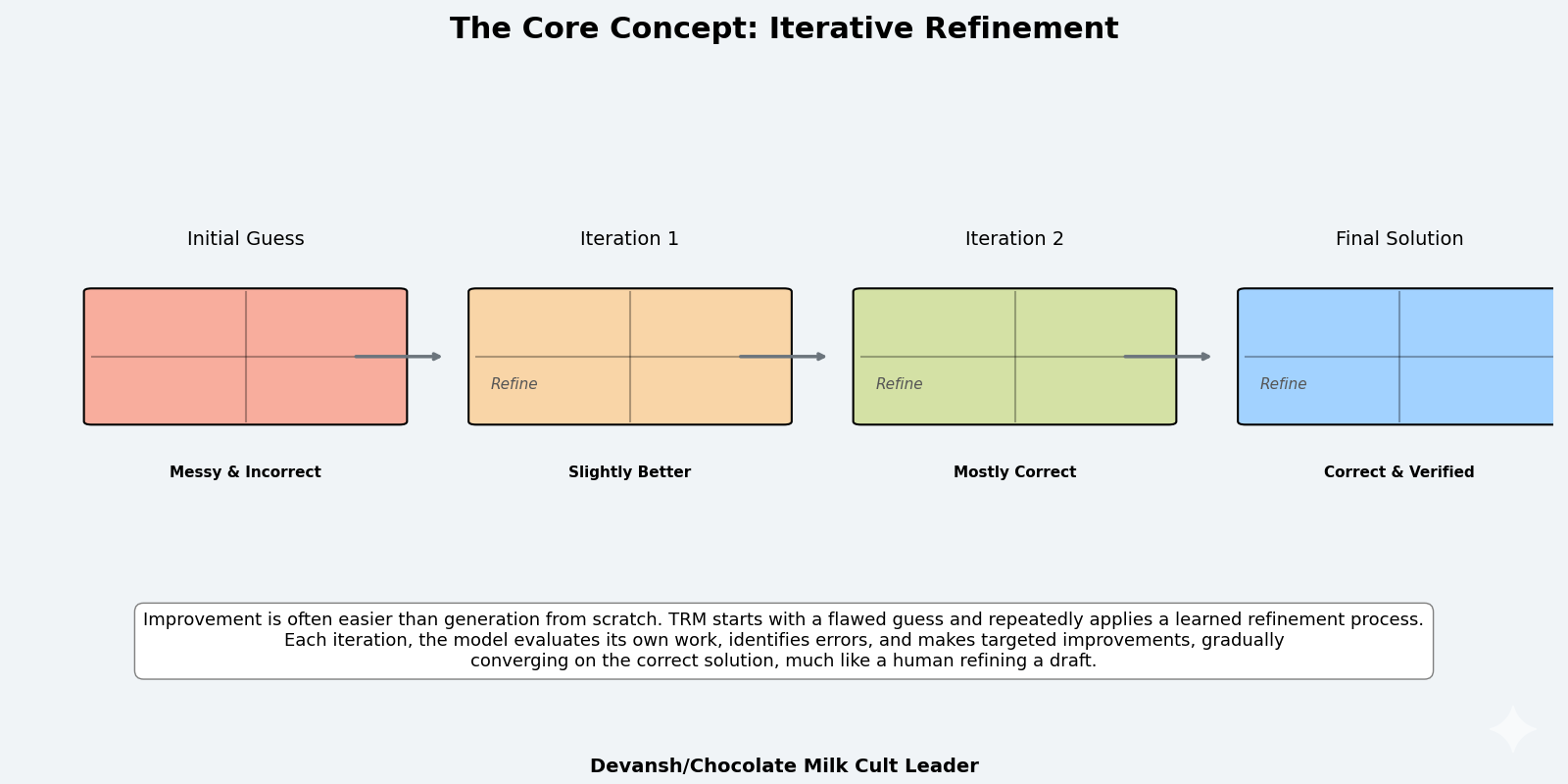
The Core Concept: Iterative Refinement
The solution is conceptually straightforward: let the model revise its answer.
Start with an initial solution — possibly random, possibly wrong. Then improve it. Check what’s wrong with the current solution and fix those errors. Repeat this process multiple times, each iteration bringing the solution closer to correct.
A human solving a difficult math problem works this way. Write down an initial approach based on guessing/past patterns/preferences. Check if it’s working. Hit a dead end. Notice an alternative path in line 3. Go back, take that path, propagate that fix forward. Check again. Find another issue. Refine. Eventually converges to the correct answer.
The key insight is that improvement is often easier than generation. Given a partially correct solution, identifying what’s wrong and fixing it can be simpler than producing the correct solution from scratch. This also aligns well with the constraints of our current AI systems, since multiple streams of research that our AI systems are MUCH better at judging then they are at generating.
This is iterative refinement: a process where a system repeatedly improves its own output. The system needs three capabilities:
Maintain a current solution state: Keep track of your current best answer
Evaluate that state: Identify what’s wrong with it
Update the state: Make targeted improvements
Critically, the system must learn to perform steps 2 and 3 — it’s not enough to hard-code “check all Sudoku constraints.” The model must learn what makes a solution better and how to make those improvements (although I see a future where we can sell specific pretrained checkers/scores as verifiers for plug-and-play usage; look up our analysis of the verifier economy for more).
This learning happens through supervision: show the model many (problem, solution) pairs and train it to refine its way from initial guesses to correct answers. This requires something very important that underpins success in many aspects of life — an ability to run a wicked 2-man.
The Architectural Requirement: Separating “Answer” from “Reasoning”
“It answers the question about why two features: remembering in context the question x, previous reasoning z, and previous answer y helps the model iterate on the next reasoning z and then the next answer y. If we were not passing the previous reasoning z, the model would forget how it got to the previous solution y (since z acts similarly as a chain-of-thought). If we were not passing the previous solution y, then the model would forget what solution it had and would be forced to store the solution y within z instead of using it for latent reasoning. Thus, we need both y and z separately, and there is no apparent reason why one would need to split z into multiple features.”
We need the model to do something different each iteration — specifically, to use information from previous iterations to guide improvement.
This requires the model to maintain two distinct types of state:
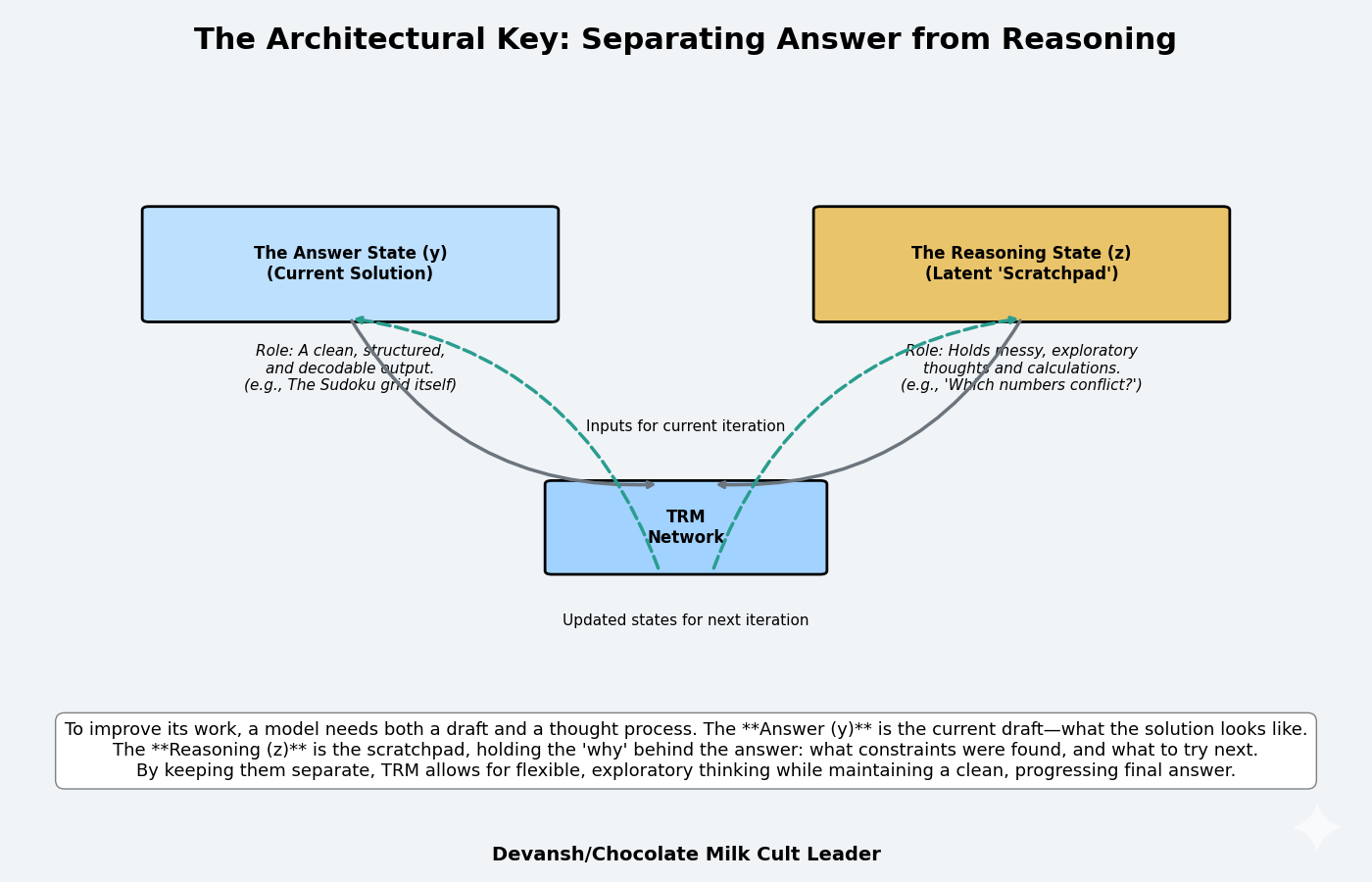
The Answer State (y): The current proposed solution. For Sudoku, this is a 9×9 grid of numbers. For maze pathfinding, this is a sequence of moves. For ARC-AGI puzzles, this is the predicted output grid. This is what the model is ultimately evaluated on — is this answer correct?
The Reasoning State (z): A latent representation of the thinking process. This is not directly interpretable as an answer, but it encodes information about how the model is analyzing the problem. Think of it as a scratchpad for intermediate calculations, explored possibilities, identified constraints, or partial insights.
Why separate these? Because conflating them restricts what the model can do.
If you only maintain y (the answer), then each iteration must update y directly. The model has no place to store intermediate reasoning. It can’t think “this approach isn’t working, let me try something else” because it has no memory of what approach it’s trying beyond what’s encoded in y itself.
If you only maintain z (reasoning), then you force the model to encode the final answer within the reasoning state. But z needs to be flexible — it should be able to represent messy, exploratory thinking. Requiring it to also encode a clean, decodable answer constrains its representation.
Separating y and z gives the model flexibility: z can be messy, exploratory, full of intermediate computations. Then, when ready, the model can extract a clean answer y from the reasoning state z. The next iteration can look at both — “here’s my current answer y and here’s how I was thinking about it z, now let me improve both.”

This is analogous to human problem-solving. You don’t solve a complex problem by iterating on the final answer alone. You maintain both your current answer draft and your understanding of why that answer might be right or wrong. The “why” guides how you revise the “what.”
The mathematical formulation is simple:
At iteration i, the model has states (yᵢ, zᵢ)
It computes improved reasoning: zᵢ₊₁ = f(x, yᵢ, zᵢ) where x is the input question
It computes improved answer: yᵢ₊₁ = g(yᵢ, zᵢ₊₁)
Repeat until convergence or maximum iterations
The model learns functions f and g through supervision on correct solutions. But this creates a new hassle.
The Training Dilemma: Deep Computational Graphs
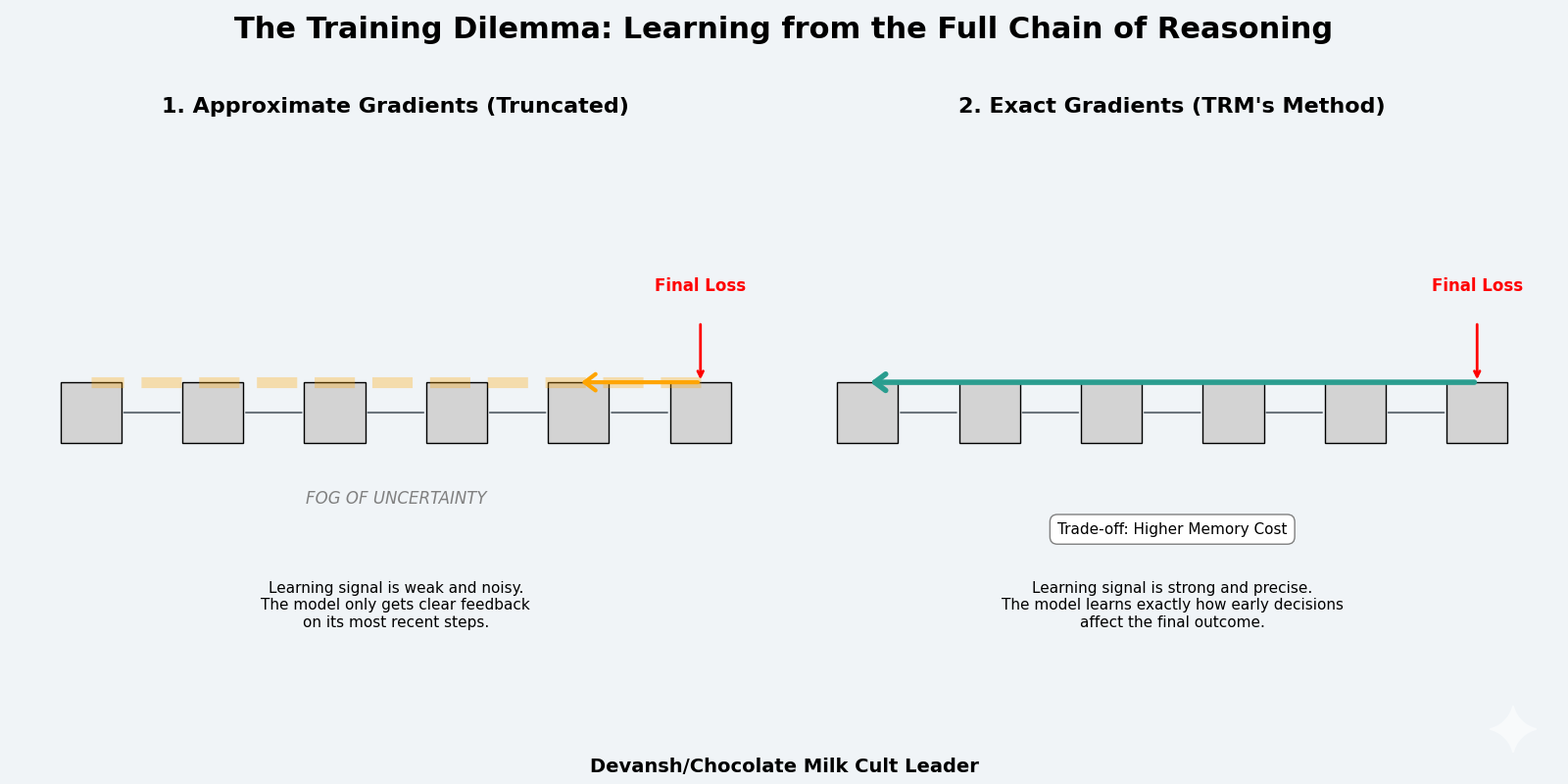
Iterative refinement creates a training problem. To learn the refinement process, you need to backpropagate through it. But unrolling multiple iterations creates an extremely deep computational graph.
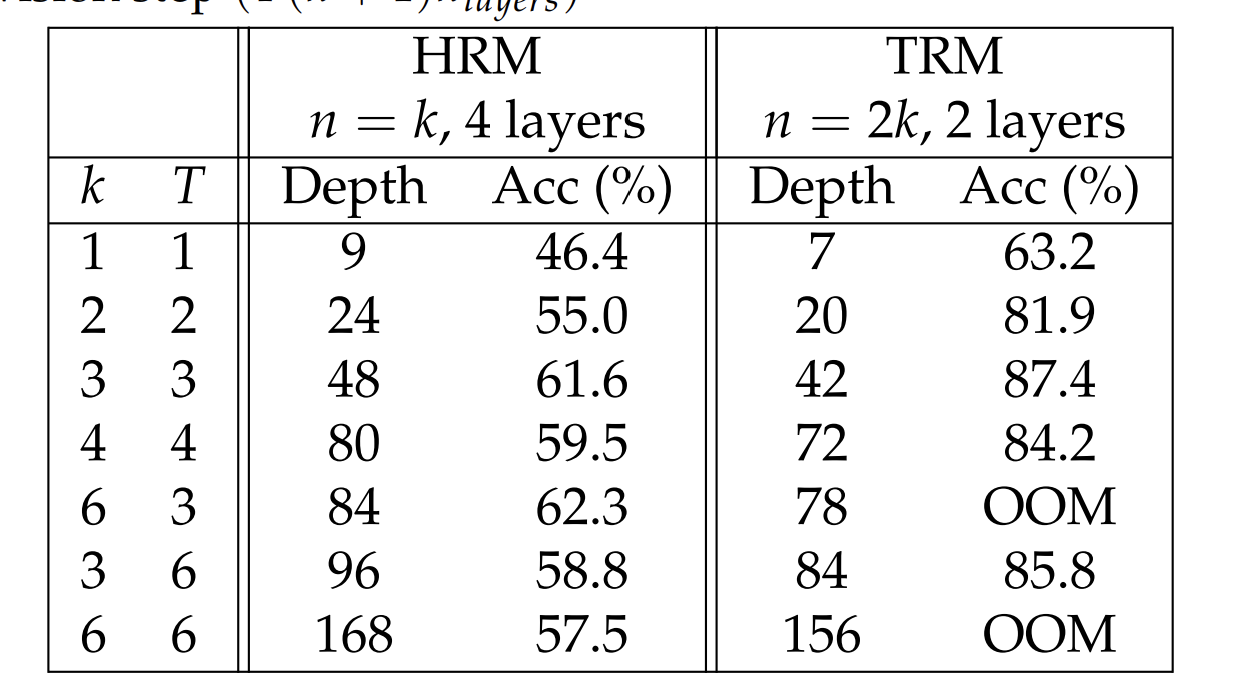
Consider 16 supervision steps, where each step performs 7 network evaluations (updating z six times, then updating y once). That’s 112 sequential network applications. If each network is 2 layers, that’s 224 layers of computation in total. Backpropagating through 224 layers requires storing all intermediate activations — every hidden state, every gradient, every tensor. This explodes memory.
Standard recurrent neural networks face this same issue, known as Backpropagation Through Time (BPTT). The solution typically involves truncating the backpropagation — only compute gradients for the last T steps, not the full sequence. This reduces memory but provides approximate gradients. The model doesn’t receive accurate learning signals about how early decisions affect final outcomes.
The alternative is to use tricks that avoid storing the full computational graph. One approach: assume the recursion converges to a fixed point, then apply the Implicit Function Theorem to compute gradients only at the equilibrium point. This is what Deep Equilibrium Models do. You assume that with enough iterations, zᵢ converges to some z* where z* = f(x, y, z*), then backpropagate through just the final step using a mathematical theorem that approximates the full gradient.
The problem: this assumes convergence actually happens. If your recursion doesn’t reach a fixed point, the theorem doesn’t apply, and your gradients are wrong. HRM (the predecessor to TRM) used this approach with a “1-step gradient approximation” — backpropagate through only the last two function calls, assuming earlier calls had reached equilibrium.
But empirical evidence from the paper shows the residuals (how much the state changes per iteration) never actually reach zero. The assumption is violated, the gradients are approximate, and performance suffers.
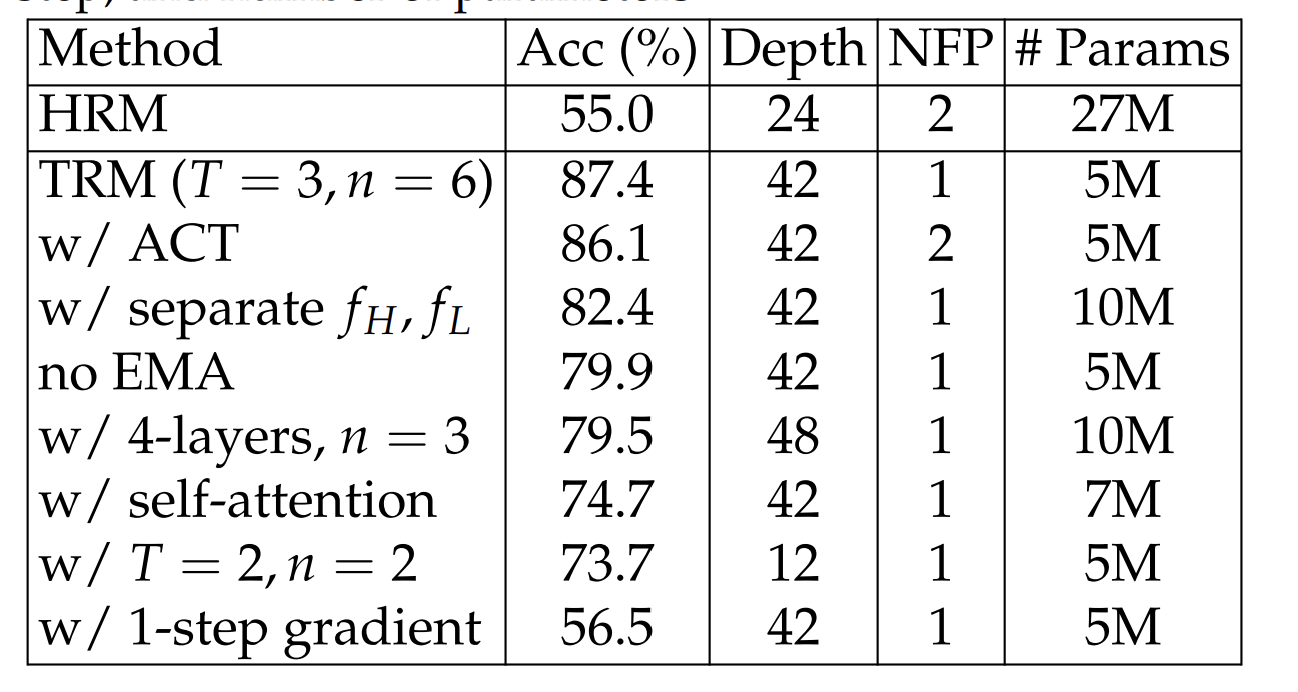
There’s a more principled alternative: just backpropagate through everything. Accept the memory cost. Store all intermediate states and compute exact gradients through the full recursion chain. This provides perfect learning signals — the model knows exactly how each refinement step contributes to the final answer.
But this is expensive. Memory scales linearly with recursion depth. But within practical limits (6–7 recursions before running out of memory), the accuracy gain is massive. On Sudoku-Extreme, full backpropagation achieves 87.4% accuracy versus 56.5% with 1-step approximation. The improved gradient signal is worth the memory cost.
The key architectural challenge is designing a system that can:
Perform iterative refinement (maintain and update y and z)
Do so through multiple cycles (recursion within each supervision step)
Stack multiple supervision steps (progressive improvement)
Train with exact gradients (full backpropagation through the recursion)
Remain small enough that this is tractable (memory doesn’t explode).
What’s life without some delusional optiMaybe if we can pull off this miracle, we can finally make Togashi finish HxH chapters on time.
Let’s look at TRM’s design directly addresses each of these requirements.
Part 3: The Blueprint of the Tiny Recursive Model
The previous section concluded with a checklist of five formidable challenges that any true reasoning architecture must overcome. TRM’s design is a direct and elegant solution to each. From a system design perspective, it’s also worth studying TRMs as a great example of a system that stacks components in a way that feed each other.
1. The Solution to State Management: A Nested Loop State Machine
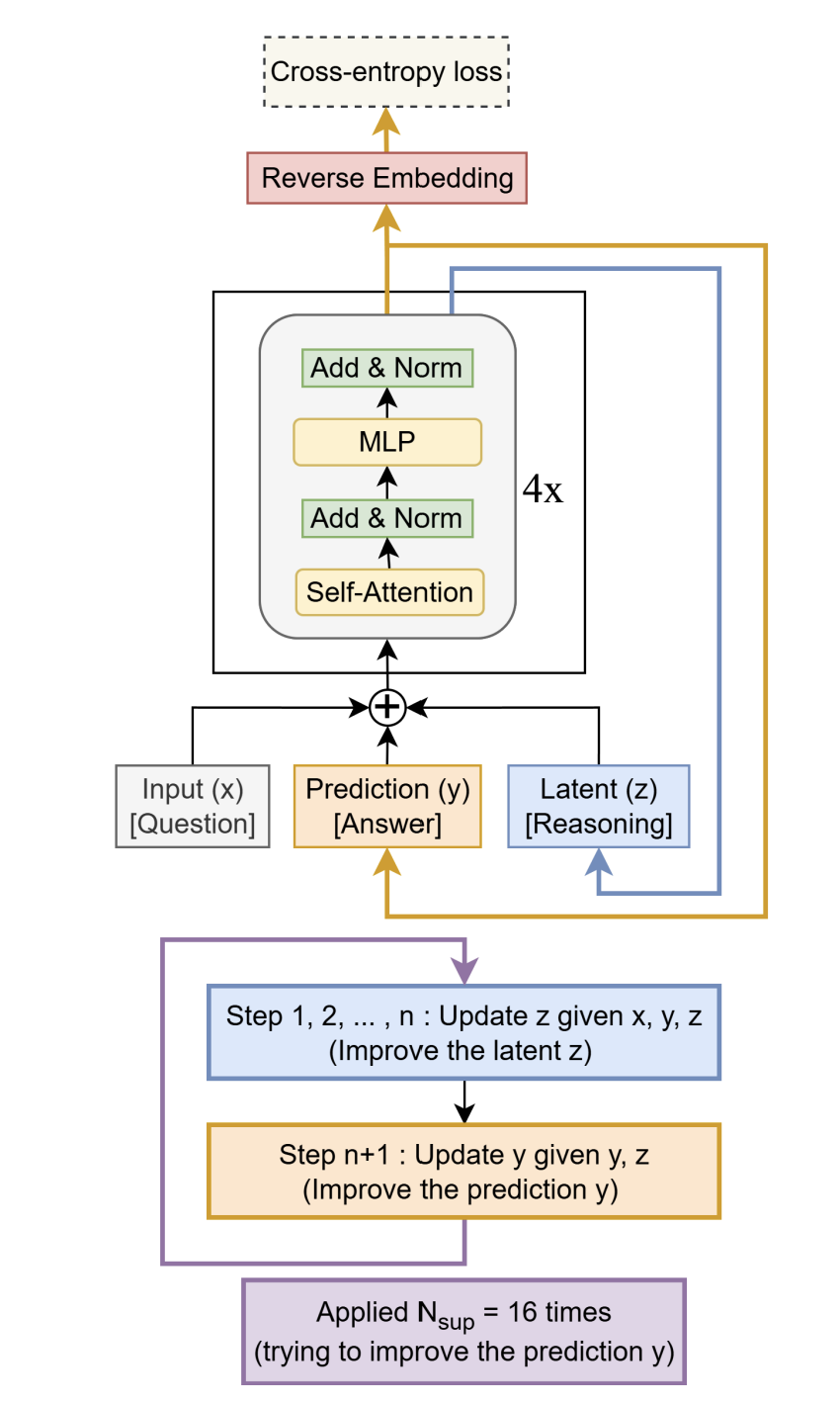
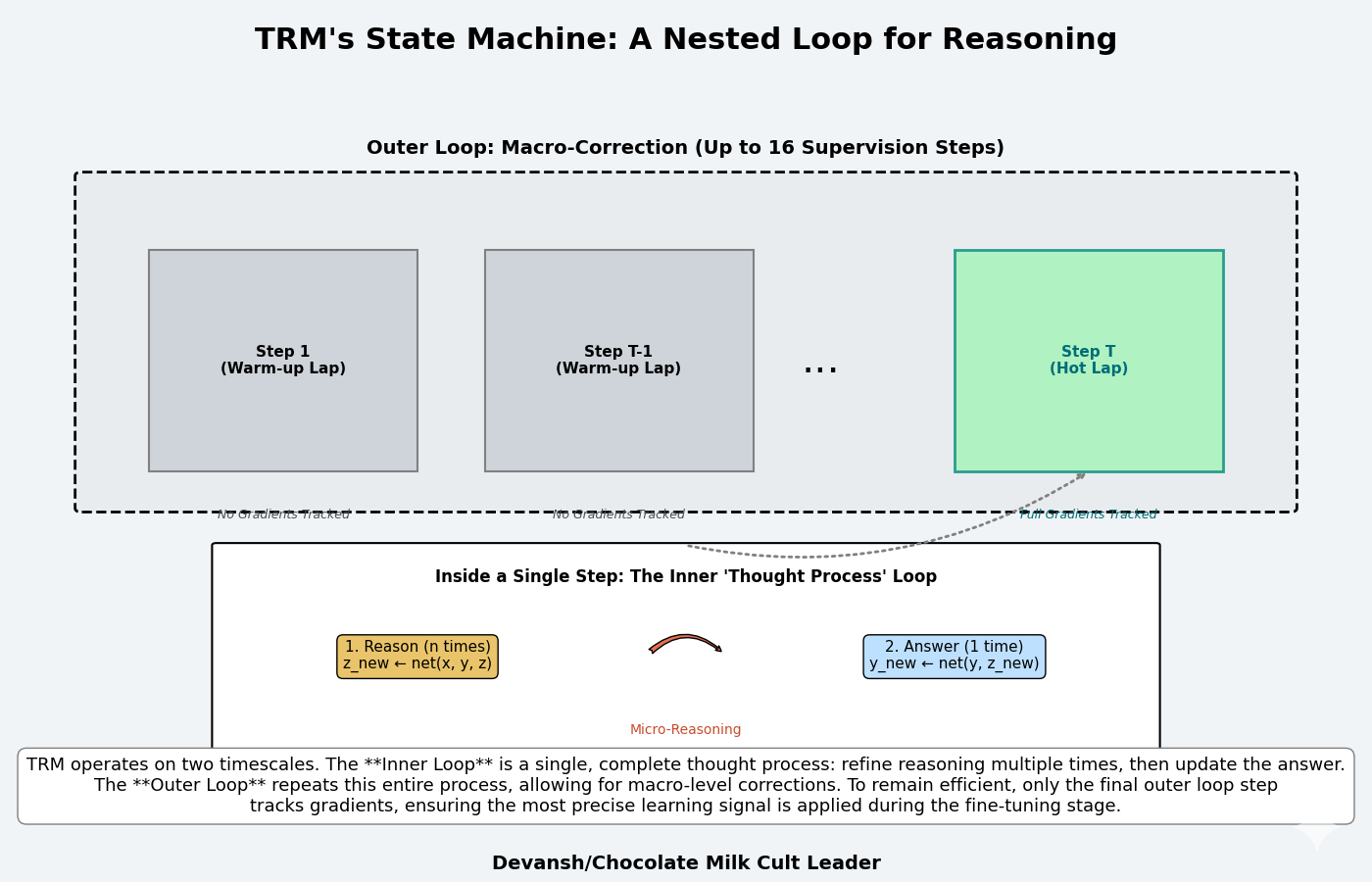
Starting ourselves in familiar territory, TRM solves the challenges of performing iterative refinement and stacking supervision steps with a nested loop structure built around a single, unified network.
The core operation is split into two concrete instructions:
Reasoning: z_new ← net(x, y, z)
Answering: y_new ← net(y, z_new)
This state machine is driven by a multi-scale computational cadence:
The Inner Loop (Micro-Reasoning): A tight loop of n reasoning instructions followed by one answering instruction. This is a single, complete thought process.
The Outer Loop (Macro-Correction): This entire thought process is repeated up to 16 times, with supervisory feedback after each one.
This deep recursion is made tractable by a key optimization. For the first T-1 outer loops, the system runs in a “warm-up” mode without tracking gradients (torch.no_grad()). This allows the model to rapidly get its answer into the right ballpark without paying the memory tax. Only the final, T-th loop is the “hot lap” — it enables full gradient tracking. This works because coarse, early-stage corrections do not require a perfect gradient; only the final, fine-tuning steps demand that level of precision.
2. The Solution to Tractability: Algorithmic Regularization
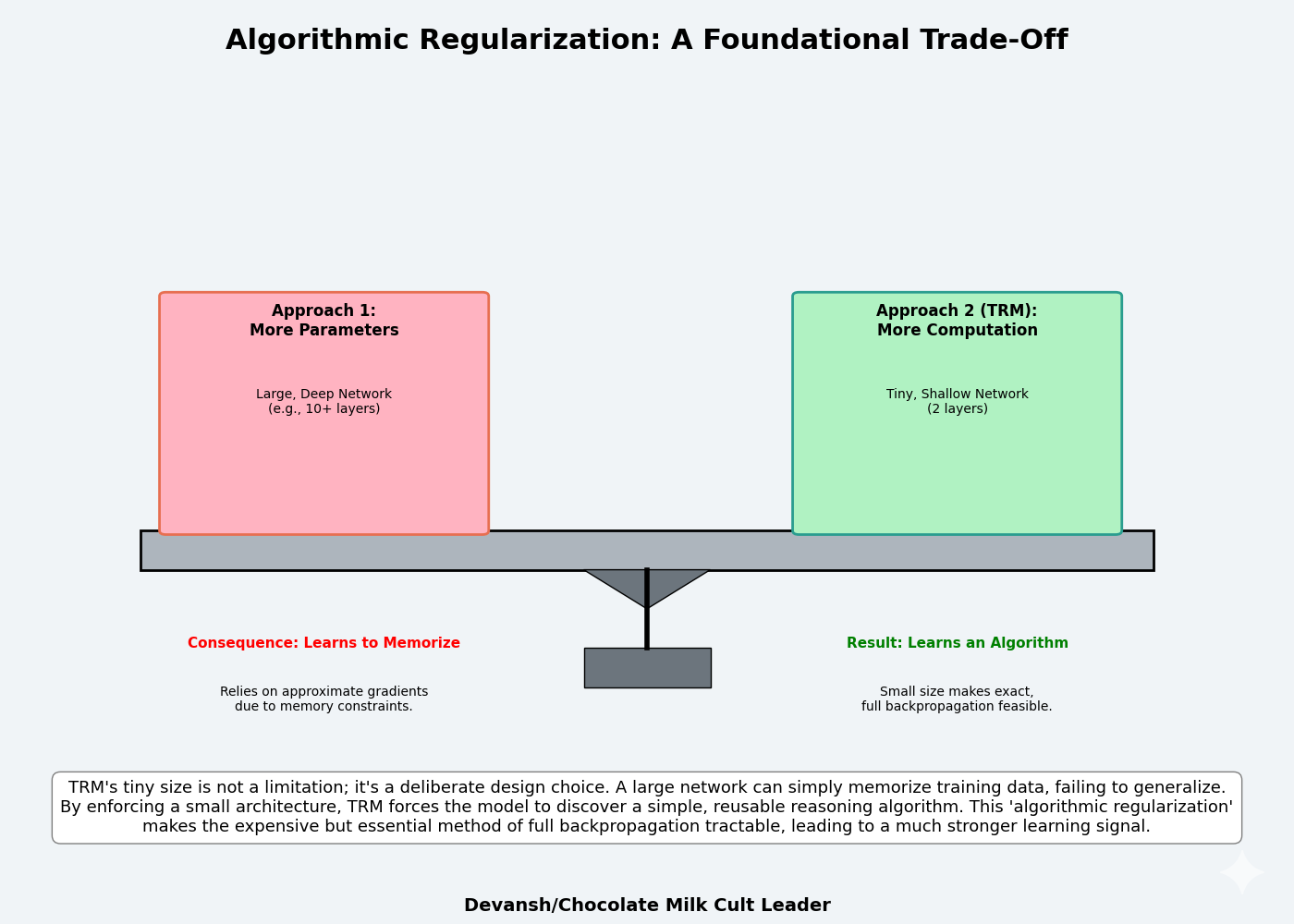
One of the more interesting design decisions made by the authors of TRM is the size of their models.
The architecture is intentionally tiny — just two transformer layers. This is a form of algorithmic regularization. A 4-layer network has enough unique parameters to encode pattern-matching lookup tables: “when I see configuration A in the training data, output B.” This works on training examples, fails on test.
A 2-layer network can’t fit the lookup table. It must compress into general rules. Recursion multiplies compute without multiplying parameters — the same 2-layer block applied 21 times per step gives 42 effective layers, but only 2 layers’ worth of unique parameters to memorize with. The model is forced to learn reusable operators: constraint propagation, conflict repair, search heuristics. These operators, composed through recursion, solve problems it’s never seen.
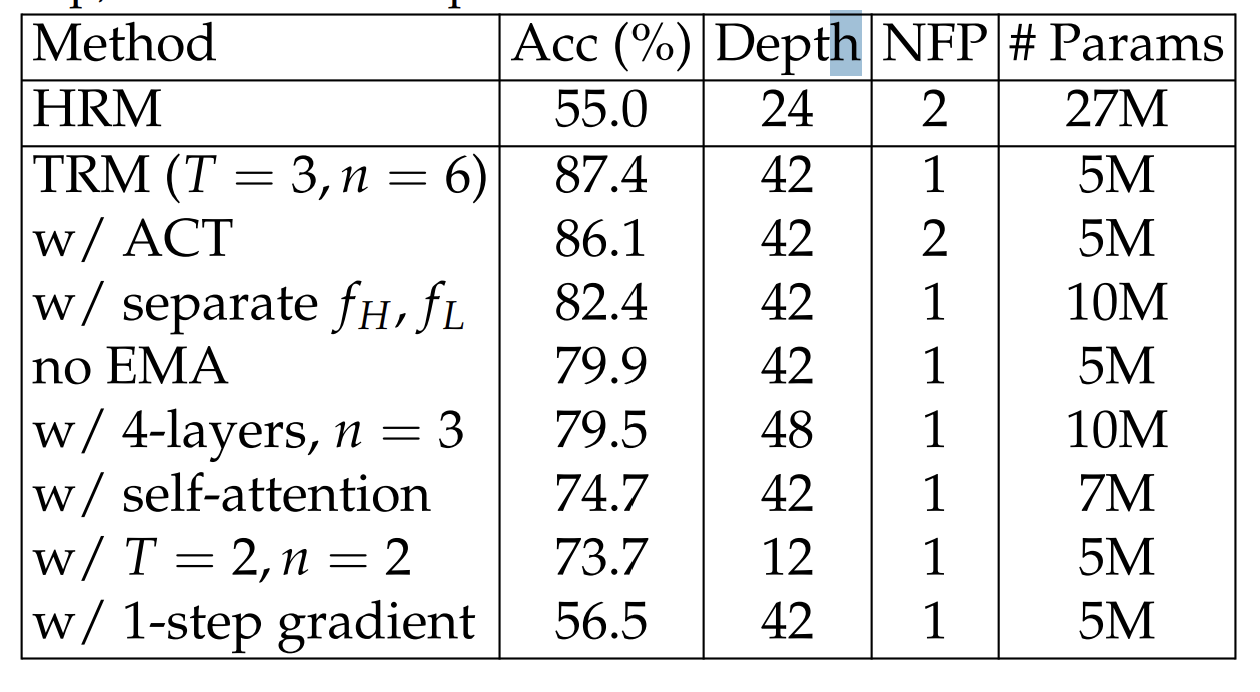
This small size is what makes the expensive but necessary full backpropagation feasible. The 30-point accuracy jump from 56.5% (with 1-step approximation) to 87.4% proves that the gradient fidelity is non-negotiable. The system accepts the constraint of a small model to afford the perfect gradient it needs to learn.
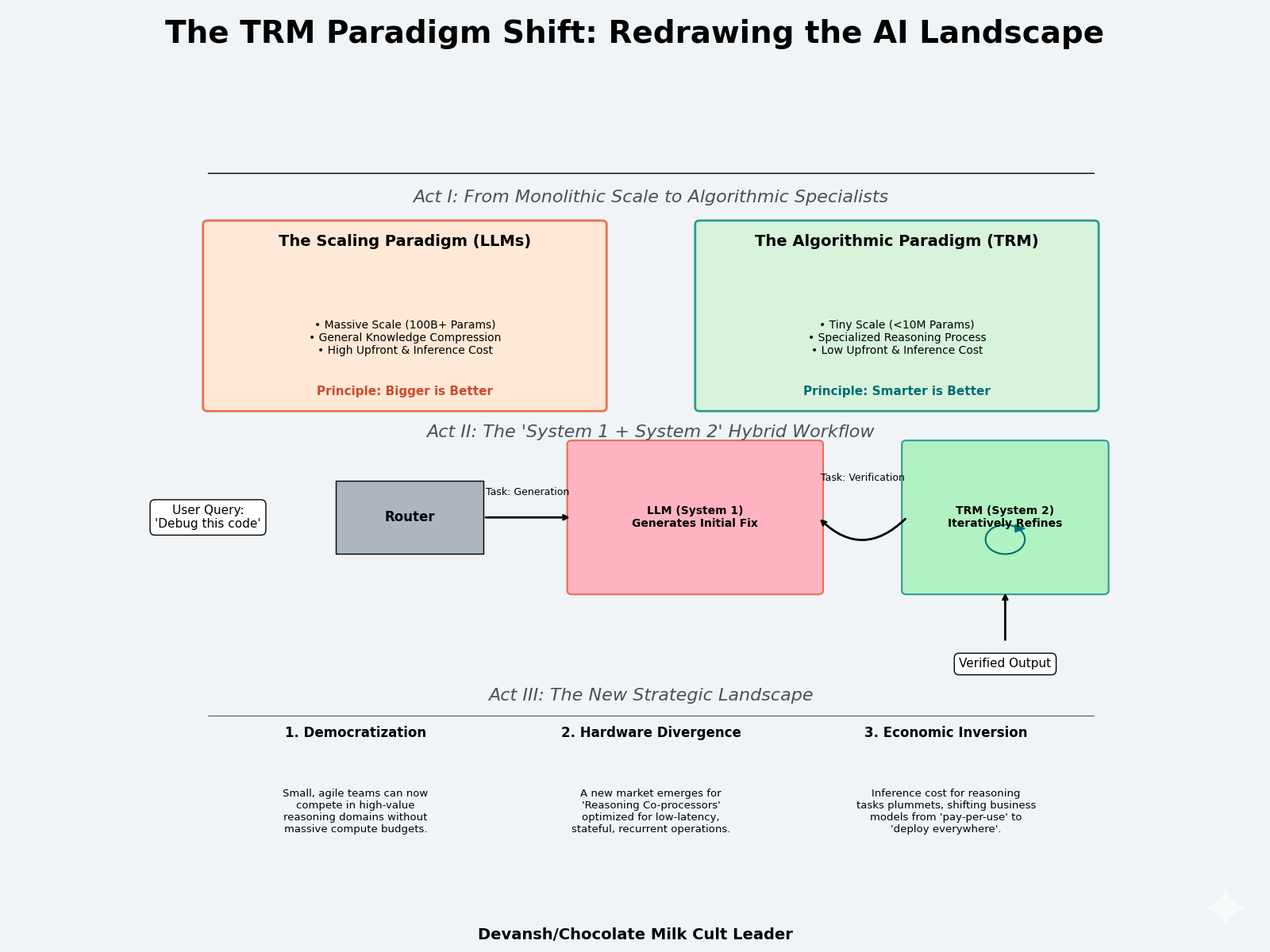
This design choice has profound implications for the future:
On Hardware: This signals a potential divergence in AI hardware. While LLMs demand massive matrix multiplication engines, TRM-like models would benefit from chips optimized for low-latency, stateful, recurrent operations. This suggests a market for “reasoning co-processors” with large amounts of fast, on-die memory (SRAM) to hold the y and z states through rapid iteration. There’s a lot of cool work being done with high-memory chips, so I expect this kind of research to explode, especially if we crack heterogeneous computing to coordinate diverse chips for the same compute.
On Future Algorithms: TRM uses a fixed recursion depth. The next frontier is making this dynamic — a model that learns to control its own computational budget, performing more reasoning steps for harder problems. Developing good early stopping mechanisms and reward signals will also be a very important component here.
On the Nature of Intelligence: This work provides strong evidence that intelligence can be an emergent property of a learned computational process, not just a function of compressed data. The value is not in the weights themselves, but in the algorithm the weights have learned to execute.
3. The Solution to Efficiency: A Smarter Halting Mechanism
To optimize the process, the model needs to know when to stop. TRM replaces a complex, two-pass Q-learning system with a simple, single-pass binary cross-entropy loss on the question: “is the current answer correct?”
Complex Q-learning halt: 86.1% accuracy, 2 forward passes.
TRM binary halt: 87.4% accuracy, 1 forward pass.
Philosophically, this works because an observable state (“have I done enough cocaine?”) is a better and more direct learning signal than an expensive, speculative lookahead (“would one more line help?”).
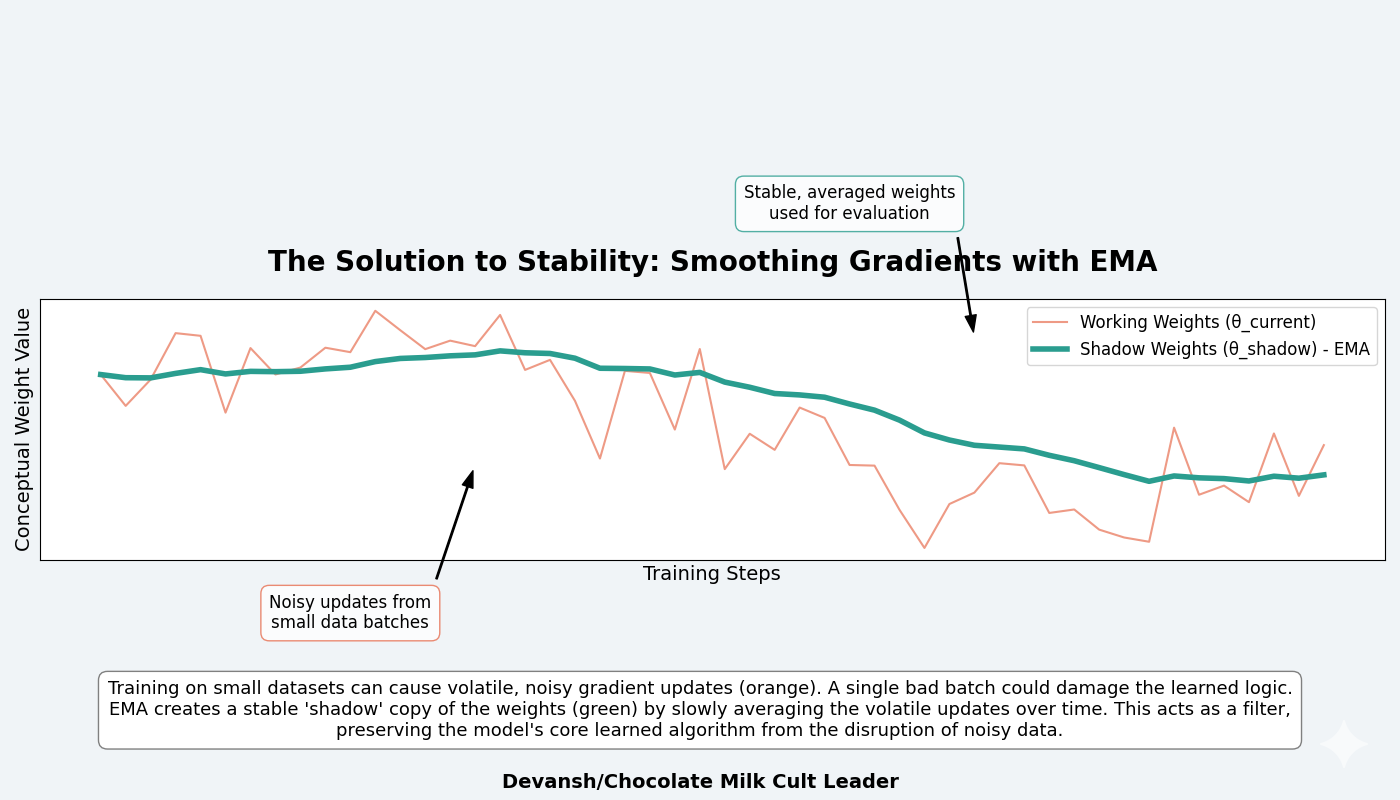
4. The Solution to Stability: Exponential Moving Average (EMA)
Training on small datasets creates high-variance gradients; a single noisy batch can push the model’s weights in a random direction, catastrophically destroying the fragile, multi-step logic it has already learned. EMA is the solution.
The technique maintains two copies of the model’s parameters:
Working Weights (θ_current): The parameters that train. These receive gradient updates every batch and are consequently volatile.
Shadow Weights (θ_shadow): A second, separate copy that updates slowly according to the rule:
θ_shadow ← 0.999 × θ_shadow + 0.001 × θ_current
In each training step, the shadow weights keep 99.9% of their previous value and absorb only 0.1% from the current trained weights. This creates a slow-moving average that acts as a low-pass filter, smoothing out the noise from individual batches. The model trains on the volatile θ_current but is evaluated using the stable θ_shadow.
The impact is massive, boosting accuracy from 79.9% to 87.4%. This 7.5 percentage point gain demonstrates that in these small-data, high-recursion regimes, preventing the model from destroying its own learned algorithm is a first-order problem. The cost is a doubling of memory for model parameters — a small price to pay for the stability that makes learning possible at all.
Overall, this seems to follow the same pattern as several other developments in computing — using more memory for superior performance. I think this is a very reasonable bet to make in the current ecosystem because most inference/hardware providers are already moving in the direction of HBM chips. This creates a nice synergy where developments in HBM (backed by billions of dollars) will passively promote this style of computing and allow these solutions to draw further attention to HBM.
Part 4: The Reality Check — Limitations and Future Directions
The Tiny Recursive Model demonstrates that small systems can think with extraordinary precision. But as with all early paradigms, the clarity of its success also exposes its limits. Understanding these boundaries is essential — both to prevent overreach and to chart the next wave of research.
1 Current Constraints of the TRM Approach
Task Specificity: TRM is a specialist, not a generalist. Its reasoning loop works when the rules of the environment are fixed and the success condition is binary — like Sudoku or pathfinding. Once the rules loosen or the objectives become fuzzy, performance collapses. This is an architectural limitation; TRM’s design assumes an explicit notion of correctness.
2. Inference Latency: Recursion trades parameter size for computation time. Each reasoning cycle adds latency; every forward pass is another “thought.” This makes TRM inherently slower than single-pass transformers. On large grids or multi-step problems, inference can balloon to seconds or minutes per sample. The future of deployment lies in adaptive halting — models that learn how many reasoning steps each problem deserves.
3. The Supervised Learning Wall: TRM’s learning signal depends entirely on supervised (problem, solution) pairs. This works for closed-form tasks, but most real-world reasoning problems don’t come with labeled ground truth. Without self-generated feedback, the system can’t extend its reasoning beyond the distribution it was trained on. To become more general, TRM must learn to critique itself — to generate, test, and verify its own answers in an unsupervised loop.
2. The Next Frontiers for Recursive Reasoning
1. Dynamic Computation: Fixed recursion depth is a relic of early design. The logical next step is adaptive iteration control: a model that determines when to stop thinking. This requires coupling the reasoning loop to a reward signal — one that optimizes for correctness per unit of compute. A model that can allocate thought dynamically would unlock a new compute–efficiency frontier.
2. Generalization to Open-Ended Tasks: If TRM can reason over puzzles, can it reason over language? The principles — state separation, iterative correction, gradient fidelity — are agnostic to domain. Future work will likely embed recursive cores inside LLMs as local “reasoning kernels.” These modules would allow generative systems to simulate deliberation before emitting text.
3. Hybrid Architectures: The endgame is hybridization: large models for perception and knowledge retrieval, small recursive engines for structured reasoning. Together they form a bidirectional loop — LLMs propose, TRMs verify, and both improve through feedback. This is the architecture of dual-process AI: fast pattern completion paired with slow deliberative correction.
3 The Meta-Lesson: What Failure Teaches
TRM’s weaknesses expose the limits of static intelligence. Every failure — overfitting to small data, excessive compute cost, domain narrowness — points to the same underlying truth: reasoning is not a property you train once; it’s a process you maintain.
Where LLMs fail because they can’t revise, TRMs fail because they can’t generalize their revision strategy. Both are incomplete halves of cognition. The synthesis — recursive reasoning operating over general world models — remains the missing piece.
A while back, I’d written about how we were experimenting with Legal Reasoning in Iqidis. Since then, we’ve refined experiments and seen great results from the following setup —
Reasoning in the latent space by using an LLM to generate initial answers. However, instead of decoding immediately, we use Evolution to generate more vectors (to simulate reasoning paths)
Using other LLMs as reward models (we directly use the vectors, we have to skip the encoding layer — since you’re already passing vectors — but this seems to be worth it).
Have a final scorer that converges chains, checks for the stopping mechanism, and then signals when our synthesis model should work.
Synthesis puts everything together.
This has allowed us to build legal reasoning that far surpasses standard foundation models without putting us through the grind of training our own models. It’s also why Iqidis has been outperforming all other legal AI competitors, including well-funded alternatives like Harvey AI.
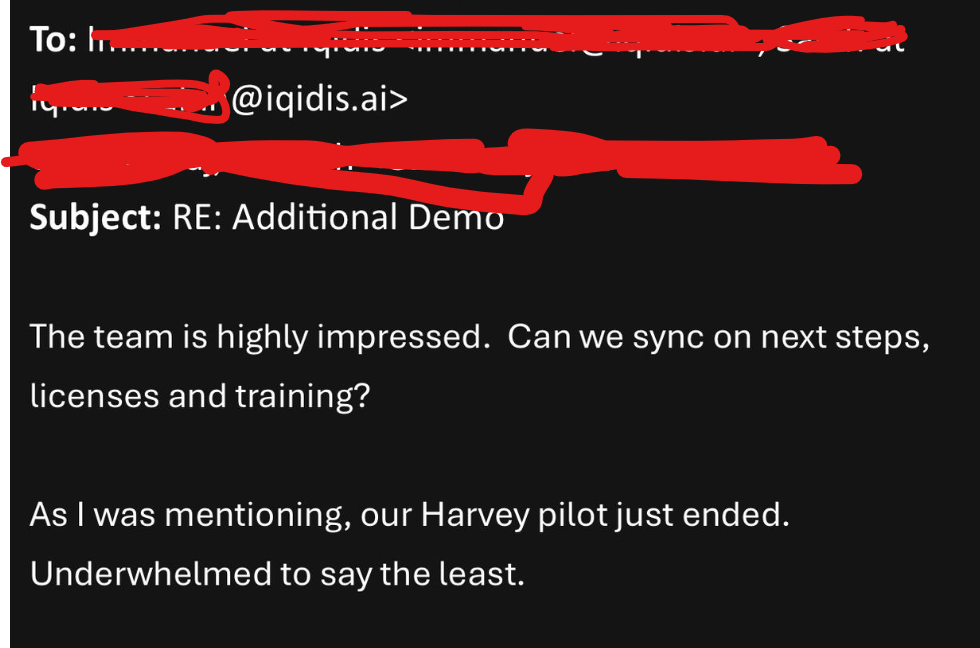
The use of general LLMs as quick reward models and solutions can help us extend TRM to general reasoning and thinking. However, several challenges related to calibration will remain. It’s an open challenge that we’re looking at actively. If you’re also looking at this space, would love to talk about how you’re seeing it.
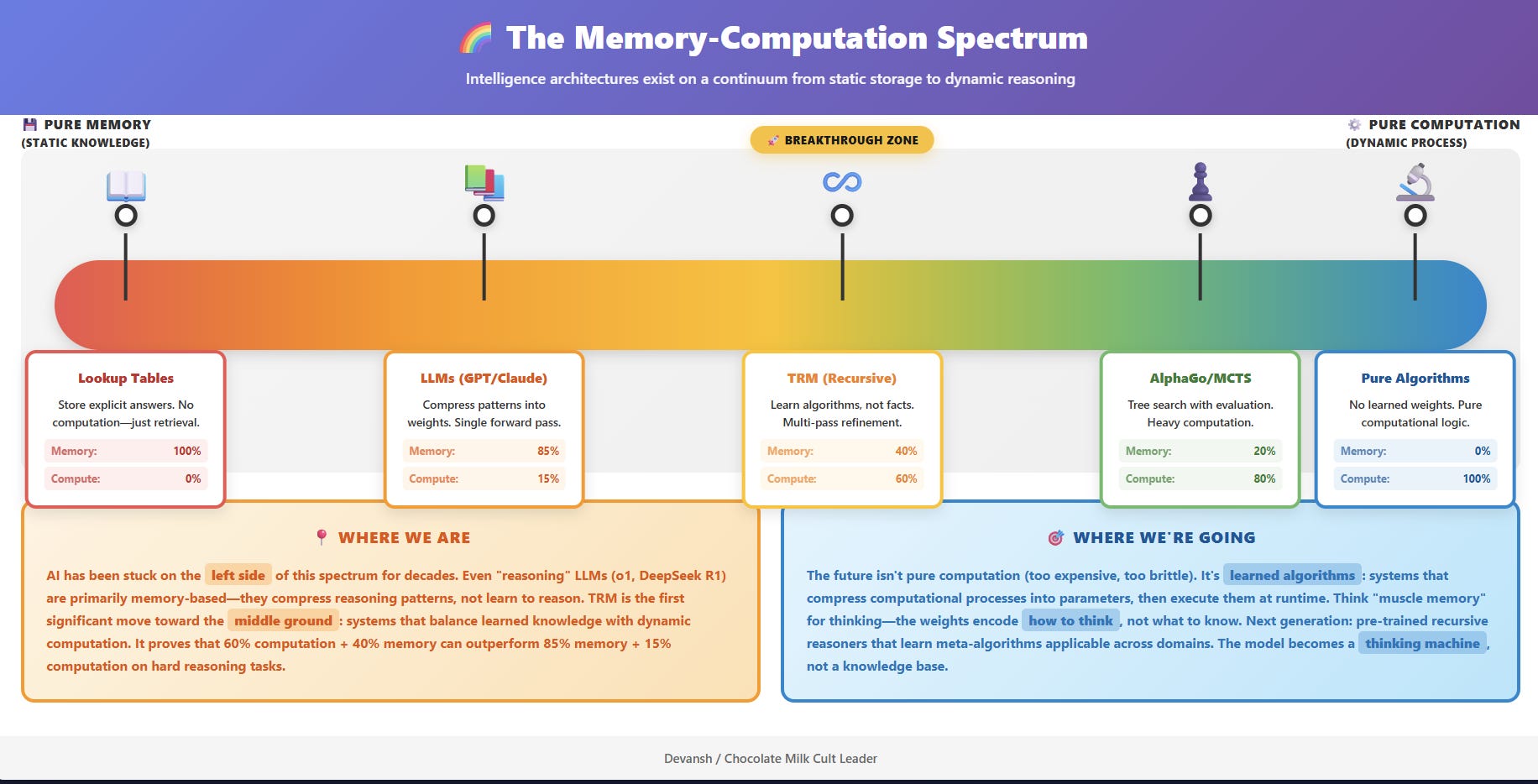
Conclusion — From Compressing Knowledge to Learning Computation
The Tiny Recursive Model does not just offer a new way to solve puzzles. It forces a redefinition of what an AI model is.
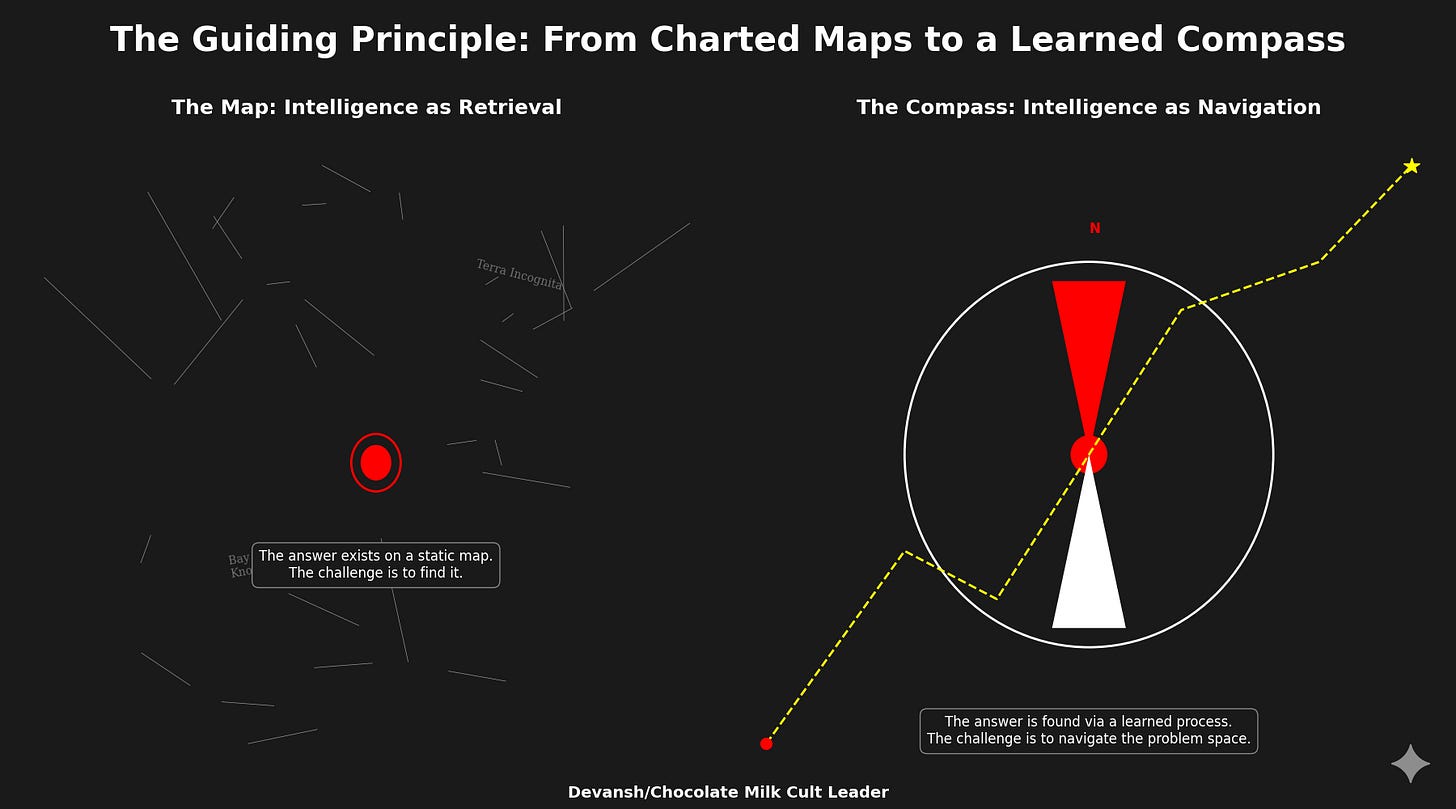
Large Language Models are fundamentally systems of compression. They distill the statistical patterns of human-generated text into a vast, static set of weights. Intelligence, in this paradigm, is a measure of how much of the world’s knowledge can be stored and recalled. It is an architecture of memory.
TRM represents a shift to systems of computation. It does not store the answer; it learns the process for finding the answer. Its parameters do not encode facts, but the steps of a reusable, verifiable algorithm. It is an architecture of thought.
This distinction reframes everything. Scaling laws optimized for data density; recursive models optimize for algorithmic depth. LLMs extend perception — TRMs extend deliberation. One captures the world; the other learns to navigate it. As architectures like TRM mature, the boundary between model and machine begins to dissolve. What matters is no longer what the system contains, but what it can repeatedly transform.
For most of AI’s history, we treated intelligence as a storage problem. The bigger the corpus, the better the mind (traditional AI did this explicitly through rules; ML does so through weights). But TRM suggests a different organizing principle: intelligence as a runtime phenomenon. A process that exists only while it is thinking — an equilibrium between error and correction, iteration and convergence. Knowledge becomes just the initial condition; computation is the act of becoming.
This shift ripples outward. In research, it means progress will be measured by the quality of reasoning loops, not the quantity of parameters. In engineering, it means architectures will be judged by how efficiently they can refine their own outputs, not how fluently they can generate text. In investment, it redefines value creation: the next trillion-dollar frontier is not larger data centers, but smaller, recursive machines that reason better per watt.
The TRM is not the endpoint — it’s the first working proof that computation itself can be learned, compressed, and repurposed. It points to a future where every model is also a mechanism, where intelligence is not embedded in weights but emerges from the structure of iteration.
We are leaving the age of memorization and entering the age of recursion — where intelligence is measured not by what it knows, but by how gracefully it can change its own mind. I’m very interested in seeing how this paradigm will build out, especially as tech-domain expert codesign become an increasing priority.
Thank you for being here, and I hope you have a wonderful day,
Dev <3
If you liked this article and wish to share it, please refer to the following guidelines.
That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow. The best way to share testimonials is to share articles and tag me in your post so I can see/share it.
Reach out to me
Use the links below to check out my other content, learn more about tutoring, reach out to me about projects, or just to say hi.
Small Snippets about Tech, AI and Machine Learning over here
AI Newsletter- https://artificialintelligencemadesimple.substack.com/
My grandma’s favorite Tech Newsletter- https://codinginterviewsmadesimple.substack.com/
My (imaginary) sister’s favorite MLOps Podcast-
Check out my other articles on Medium. :
https://machine-learning-made-simple.medium.com/
My YouTube: https://www.youtube.com/@ChocolateMilkCultLeader/
Reach out to me on LinkedIn. Let’s connect: https://www.linkedin.com/in/devansh-devansh-516004168/
My Instagram: https://www.instagram.com/iseethings404/
My Twitter: https://twitter.com/Machine01776819



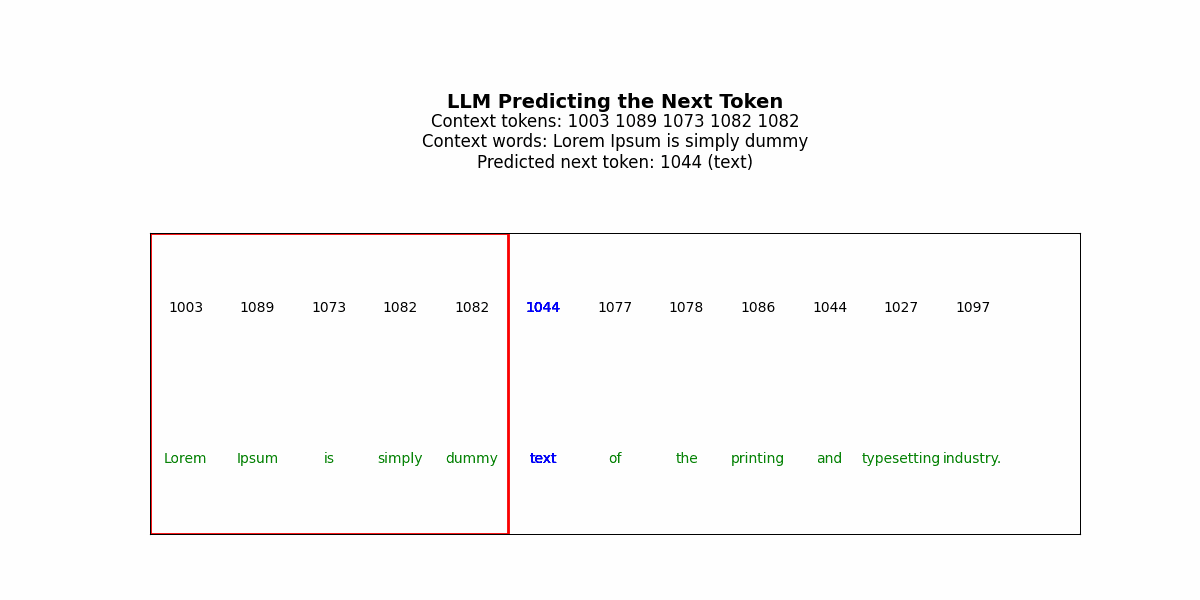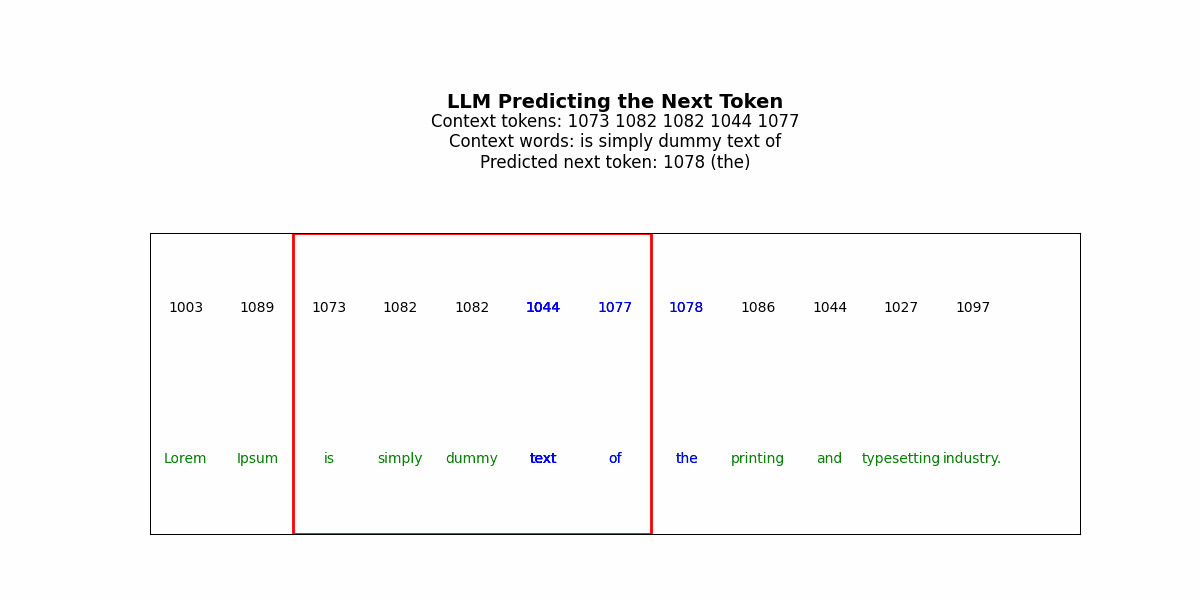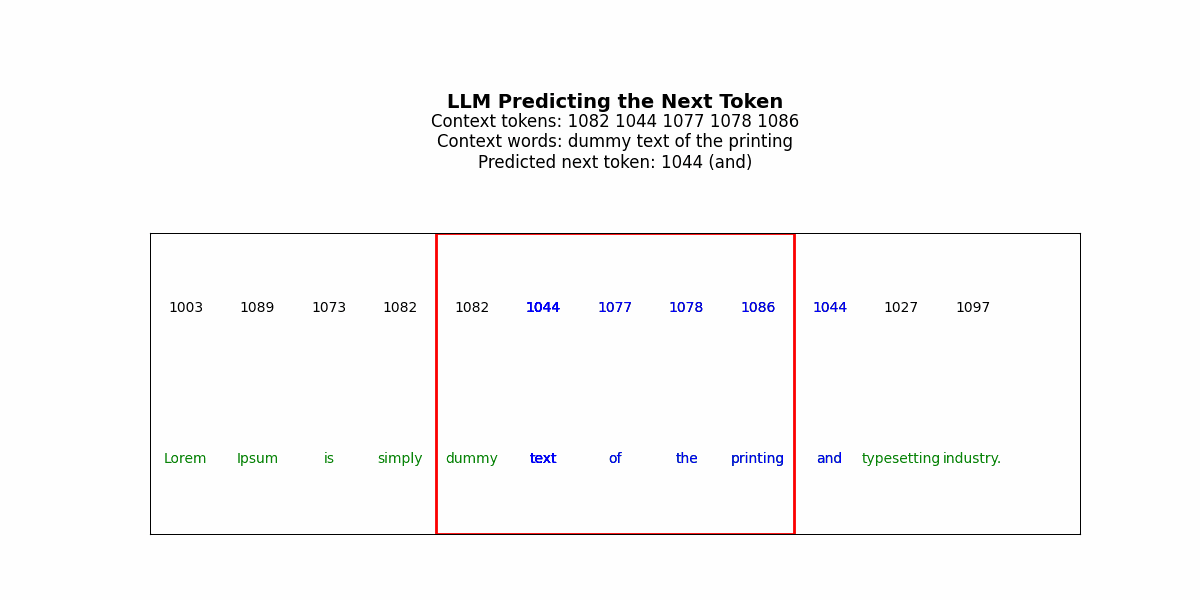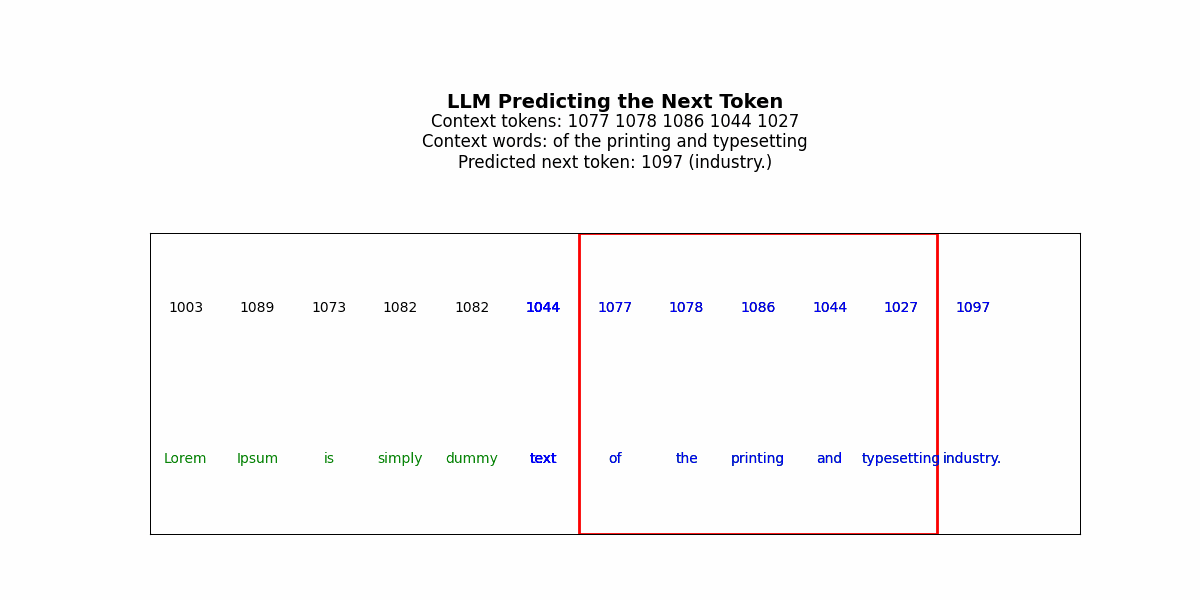





The architecture section remind me of auto encoders. Where the bottle neck is there so that model learns general rules instead of only pattern matching.
is there any open source code for TRM?